Texnik tizimlarda axborot texnalogiyalari

Tayanch so’z va iboralar: Matlab, MathCad, Colculator, Graph , Matrix , Evluation, Colculus, if operatori,switch operatori,for ,while,break operatori

• Iqtisodiy masalalarni echishda, mashinasozlikda, aviasozlikda, kosmosni tadqiq qilishda, texnologik jarayonlarni optimallashtirishda, ishlab chiqarishni boshqarish va rejalashtirishda; EHM da biror bir amaliy masalani echish uchun oldin u «matematik tilga» ko‘chirilishi talab etiladi: Real ob’ekt, jarayon yoki tizimning matematik modeli qurilishi lozim bo‘ladi. Model so‘zi lotincha modulus so‘zidan kelib chiqqan bo‘lib, u nusxa, obraz, tavsir degan ma’noni anglatadi.

Modellashtirish deb - biror A ob’ektni boshqa B ob’ektga almashtirishga aytiladi. Almashtiriladigan real ob’ekt A asl (original) deb, almashgan ob’ekt esa model deb aytiladi.

Modelning mukammalligi bo‘yicha fikrlar Model haqida Norbert Viner va Arturo Rozenblatni fikri: “Mushukning eng yaxshi modeli bo‘lib, boshqa mushuk hisoblanadi, undan ham yaxshiroqg‘i bu o‘sha mushukning o‘zidir”. YAna bir misol: “CHarli CHaplin harakatlarini taqlid qilish bo‘yicha tanlov o‘tkazilib, mazkur tanlovda CHarli CHaplinning o‘zi xam ishtirok etgan va ikkinchi o‘rinni egallagan”. Nega? Modellashtirish maqsadi: O‘rganilayotgan ob’ekt, jarayon va tizimning u yoki bu xususiyatlarini o‘rganish, ular haqida to‘laroq ma’lumot olish, ularni qayta ishlash, tasvirlash va ulardan foydalanish; А B Bunda model ob’ektni o‘rganish vositasi sifatida qo‘llaniladi. Modellashtirish nazariyasi o‘rganilayotgan ob’ektlarni boshqa ob’ekt - modelga almashtirish orqali mazkur asl-ob’ektlarning xususiyatlarini tadqiq qilish usullarini o‘rganadi.

Modellarni 2 sinfga ajratish mumkin:

• Moddiy yoki Real (moddiy, tabiatda mavjud),

• Mavhum yoki Ideal yoki Abstrakt (tabiatda mavjud emas). Real modellar:

• Tabiiy (natural),

• fizik,

• matematik. Ideal (mavhum) modellar:

• ko‘rgazmali,

• timsolli,

• matematik.

Real natural modellar – bu o‘rganilayotgan hamda ilmiy, texnik va ishlab chiqarish sinovlari o‘tkazilayotgan real ob’ektlar, jarayonlar, tizimlar ya’ni asl ob’ekt.

Real fizik modellar – bu asl-ob’ektlarning biror fizik xususiyatlarini tasvirlovchi maketlar, mulyajlar va boshqalar.

Real matematik modellar – bu asl ob’ektning biror matematik xususiyati yoki xossasini tasvirlovchi analogli, tarkibli, geometrik, grafik, raqamli ob’ektlar.

Ideal (mavhum) ko‘rgazmali modellar – bu sxamalar, xaritalar, chizmalar, grafiklar va boshqa modellar.

Ideal (mavhum) timsolli modellar – bu belgilar, timsollar, alfavit, dasturlash tillari va boshqalar.

Ideal (mavhum) matematik modellar – bu analitik, funksional, imitatsion(taqlidli) va boshqa modellar.

Real natural modellardan tashqari barcha modellar insonning abstrakt tafakkuri mahsuli hisoblanadi

Matematik modellashtirish - bu ob’ekt, jarayon yoki tizimni matematik modelga amlashtirish orqali uning xususiyatlarini o‘rganish vositasi. Matematik model - bu ob’ekt, jarayon yoki tizimning qaysidir xususiyatlarini o‘rganishga qulay bo‘lgan, matematik tilda tasirlangan model. Umumiy holda matematik model quyidagicha ifodalanadi F ( X, Y, Z, t) = 0 Bu erda X – kirish ma’lumotlarini tasvirlovchi o‘zgaruvchi vektor, Y – chiqish ma’lumotlarini tasvirlovchi o‘zgaruvchi vektor, Z – tashqi ta’sirlarni ifodalovchi vetor, t - vaqt Matematik modellar tuzilish tamoyillariga ko‘ra:

- Analitik

- Imitatsion (taqlid) modellarga bo‘linadi Analitik modellarda – real ob’ektlar, jarayonlar va tizimlarning ishlash jarayonlari aniq funksional bog‘lanishlar (matematik formulalar) ko‘rinishida yoziladi Analitik modellar:

• Tenglamalar (algebraik, transsendent, differensial, integral tenglamalar)

• Approksimatsiya masalalari (interpolyasiya, ekstropolyasiya, sonli differensiallash va integrallash)

• Optimizatsiya masallari

• Stoxastik masalalar Lekin o‘rganilayotgan ob’ektlar murakkablashgan sari ularning analitik modellari qurish va tadqiq qilish qiyin masalaga aylanadi. SHuning uchun bunday ob’ektlarning imitatsion modellariga murojat qilinadi Imitatsion modellarda o‘rganilayotgan ob’ekt, jarayon va tizimlarning ishlashi qandaydir algoritmlar bilan almashtiriladi. Algoritmlar o‘rganilayotgan ob’ekt, jarayon va tizimlar ishini ularning mantiqiy tuzilishi va vaqt davomida kechishini saqlagan holda kichik elementlarga bo‘lgan holda imitatsiya, ya’ni taqlid qiladi. Boshqacha qilib aytganda, imitatsion modellar ob’ekt, jarayon va tizimlar ishini imitatsiya (taqlid) qiladigan matematik modellar ustida kompyuterda o‘tkaziladigan hisoblash eksperimentlari ya’ni tajribalaridir. Matematik modellar o‘rganilayotgan ob’ekt, jarayon va tizimlar xususiyatlariga ko‘ra:

- Diterminal

- Stoxastik modellarga bo‘linadi Diterminal modellarda – o‘rganilayotgan real ob’ektlar, jarayonlar va tizimlarning ishlashida tasodifiy ta’sirlar bo‘lmaydi. Ularning o‘zini tutishini aniq funksional bohlanishlar orqali ifodalash mumkin bo‘ladi. Stoxastik modellarda esa o‘rganilayotgan real ob’ektlar, jarayonlar va tizimlarning ishlashida tasodifiy ta’sirlar mavjud bo‘ladi. Ularning o‘zini tutishini ehtimollar nazariyasi va matematik statistika metodlari asosida ifodalanadi. Matematik modellar kirish ma’lumotlarining tipiga qarab:

- Uzluksiz

- Diskret modellarga bo‘linadi Agar kirish ma’lumotlari va parametrlari uzluksiz va matematik bog‘lanishlar turg‘un bo‘lsa, bunday modellar uzluksiz modellar deb aytiladi. Agar kirish ma’lumotlari va parametrlari diskret va matematik bog‘lanishlar turg‘un bo‘lmasa, bunday modellar diskret modellar deb aytiladi. Matematik modellar vaqtga nisbatan o‘zini tutishiga qarab:

- Statik

- Dinamik modellarga bo‘linadi Statik modellar ob’ekt, jarayon va tizimlarning biror muayyan vaqt momentidagi o‘zini tutishini tasvirlaydi, ya’ni vaqtga bog‘liq bo‘lmaydi Dinamik modellar ob’ekt, jarayon va tizimlarning vaqt bo‘yicha o‘zgarishini tasvirlaydi Matematik modellashtirishning asosiy bosqichlari:

• Maqsadlarni shakllantirish;

• Ob’etni o‘rganish

• Matnli modellashtrish (masalaning qo‘yilishini so‘zlar bilan ifodalash)

• Matematik modellashtirish

• Masalani yechish usulini tanlash

• Masalani yechish dastur tilini tanlash va dasturni yozish

• Kompyuterda masalani echish

• Topilgan yechimni tahlil qilish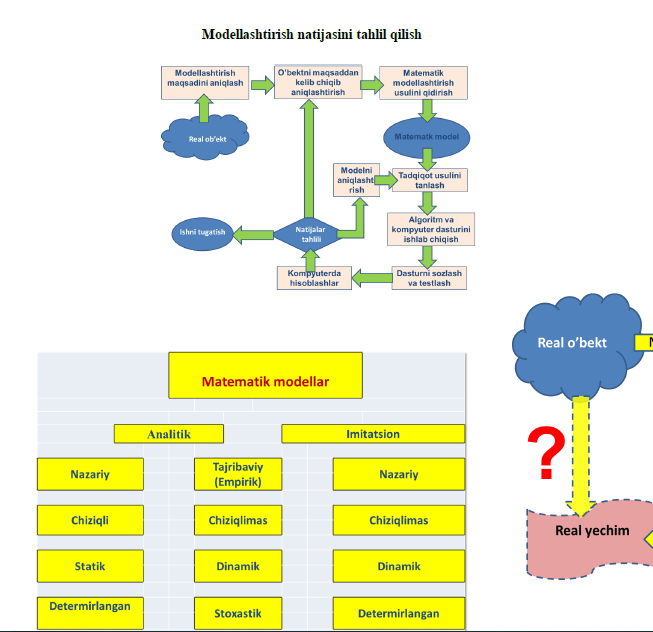

Matlab tizimi haqida umumiy tushuncha

Matlab tizimi haqida umumiy tushuncha MATLAB-Matrix LaboratoryMatlabning 1-lahjasi 70-yillarning oxirlarida Nyu-Meksika va Stanford universitetida yozilib, matritsalar nazariyasi, chiziqli algebra, sonlar tahlili kursidan dars berish uchun qo’llanilgan. Hozir tizimning imkoniyatlari keng darajada oshgan. Hozirda Matlab - bu muxandislik va ilmiy hisoblarning yuqori samarali tili. U matematik hisoblar, ilmiy grafikani vizuallashtirish va dasturlashni ta’minlaydi. Matlab tizimi ko’proq qo’llaniladigan sohalar:

• matematika va hisoblash

• algoritmlarni qayta ishlash

• hisoblash eksperimenti, modellashtirish imitatsiyasi, maketlash

• berilganlarni tahlil qilish va natijalarni vizuallashtirish

• ilmiy va muhandislik grafikasi

• amaliyot dasturlarini qayta ishlash Matlab - bu shunday interfaol (bevosita) tizimki, undagi asosiy ob’ekt bo’lgan massivning o’lchamlarini aniq yozish talab qilinmaydi. Bu esa juda ko’p hisoblashlarni(vektor, matritsa ko’rinishidagi) tez vaqtda yechish imkonini beradi. Shuning uchun Matlabda xotirani dinamik taqsimlash evaziga C va Fortran tillaridagiga qaraganda amallar bajarish osonroq kechadi. Matlab tizimi bu ham amaliyot muhit, ham dasturlash tilidir. Tizimning eng kuchli tomonlaridan biri bu Matlab tilida ko’p marta foydalaniladigan dasturlar yozish mumkin. Matlab tizimining yordam lahjasidan foydalanish mumkin va Adobe Acrobat yordamida PDF formatda chop qilish mumkin. Adobe Acrobat tahrirlovchisi matnni har xil shriftlarda, grafika va tasvirlar bilan kitobni o’qish imkonini beradi. Agarda kompyuter Internet tarmog’iga ulangan bo’lsa, Matlab tizimi varag’iga chiqish mumkin. Amaliy dasturlar paketi Matlab tizimida amaliy dasturlar paketi mavjud:

• Notebook

• Symbolic Mathematics Toolbox

• Control Systems Toolbox

• Signal Processing Toolbox

Matlab tizimining dastur ta’minoti tarkibiga “tirik” kitob (MS Word tahrirlovchisi muhitidan) yaratish uchun yangi vosita qo’shilgan. Amaliy dasturlar paketi Notebook shunday vositadir. Amaliy dasturlar paketi Notebook muhitida yaratilgan M-kitob deb ataladi. M-kitobda matnlar, Matlab tizimi buyruqlari va ularning bajarilish natijalari joylashgan. M-kitobni yaratish yoki tahrirlashda Word tahrirlovchisi M-book maxsus shablonidan foydalanadi. Bu shablon Word tahrirlovchisi idan Matlab tizimiga kirish va uni formatlashni boshqarish imkonini beradi. Amaliy dasturlar paketi Notebook bilan ishlash uchun Word tahrirlovchisini yuklash kerak va yangi M-kitob ochish yoki mavjud M-kitobni tahrirlash kerak. Word tahrirlovchisi ini M-kitobga aylantirish mumkin. M-kitobga matn kiritish Word tahrirlovchisida matn kiritishdan farq qilmaydi. Matlab tizimi buyruqlari va operatorlarini yozish uchun maxsus kataklardan foydalaniladi. Bu buyruq va operatorlarni matn ichida ham joylashtirish mumkin. M-kitob bilan ishlashda amaliy dasturlar paketi Notebookning quyidagi buyruqlaridan foydalanish mumkin:

• Define Input Cell (kiritish yacheykasini yaratish)

• Define AutoInit Cell (avtostart yacheykasini yaratish)

• Define Calc Zone (hisoblash zonasini yaratish)

• Undefine Cells (yacheykani matnga akslantirish)

• Purge Output Cells (chiqarish yacheykasini o’chirish) • Group Cells (ko’p satrli kiritish yacheykasini yaratish)

• Ungroup Cells (yacheykalar guruhini kiritish yacheykasiga akslantirish)

• Hide/Show Cell Markers (yacheyka markerlarini yashirish/ko’rsatish)

• Toggle Graph Output for Cell (grafika chiqarishni ta’qiqlash/ruxsat berish)

• Evaluate Cell (yacheykani hisoblash)

• Evaluate Calc Zone (zonani hisoblash)

• Evaluate M-book (M-kitobni hisoblash)

• Evaluate Loop (kiritish yacheykasini takrorlashda hisoblash)

• Bring MATLAB to Front (Matlab buyruqlar darchasini 1-bo’lib ko’rinadigan holga keltirish)

• Notebook Options (M-kitobdagi hisoblash natijalarini terminalga chiqarishni boshqarish) Matlabni yuklash uchun PC yoki Mac da Matlab belgisi ustida sichqoncha ko’rsatkichini ikki marta bosish kerak. Uni Unix tizimida yuklash uchun amaliyot tizim satrida Matlab buyrug’ini berish kerak. Matlabdan chiqish uchun Matlab satrida quit buyrug’ini berish kerak. Grafikni chop etish File tavsiyanomasidagi Print optsiyasi va print buyrug’i yordamida Matlab tizimida chizilgan grafiklar chop qilinadi. Print tavsiyanomasi muloqat darchasini chaqiradi. Bu darcha bosmaga chiqarishning odatdagidek har xil variantlarini tanlash imkonini beradi. Print buyrug’i M-fayllarni bosmaga chiqarishni nazorat qilishni ta’minlaydi. Natija printerga jo’natilishi mumkin yoki berilgan faylda saqlanishi mumkin. Oqimlarni boshqarish Matlab oqimlarni boshqarish tarkiblarining 5 ta ko’rinishini o’z ichiga oladi:

• if operatori

• switch operatori

• for takrorlanishi

• while takrorlanishi

• break operatori If operatori - agar ifoda rost qiymat qabul qilsa, mantiqiy ifodani hisoblaydi va operatorlar guruhini bajaradi. Switch operatori - ifoda yoki o’zgaruvchilar qiymatida operatorlar guruhini bajaradi. Case va otherwise kalit so’zlari bu guruhlarni ajratadi. Faqat birinchi mos keluvchi hol bajariladi. Switch operatoridan foydalanganda end dan ham foydalanish kerak. For takrorlanishi - operatorlar guruhini oldindan qayd qilingan son marta takrorlaydi. While takrorlanishi - mantiqiy shart bajarilganga qadar operatorlar guruhini ma’lum son marta takrorlaydi. Break operatori - for yoki while takrorlanishidan chiqib ketishni ta’minlaydi. M-fayllar Matlab tili kodlarini o’z ichiga olgan fayllar M-fayllar deb ataladi. M-fayllarni yaratishda matn tahrirlovchilaridan foydalaniladi. M-fayllarning ikkita turi mavjud:

• Stsenariylar;

• Funktsiyalar. Stsenariylar kiruvchi va chiquvchi argumentlarga ega emas, ular ko’p marta bajarilishi kerak bo’lgan qadamlar ketma-ketligini avtomatlashtirish uchun qo’llaniladi. Funktsiyalar kiruvchi va chiquvchi argumentlarga ega. Matlab tili (funktsiyalar kutubxonasi, amaliy dasturlar paketi) imkoniyatlarini kengaytirish uchun qo’llaniladi. Boshqariluvchi grafika Matlab sirtlar, chiziqlar va boshqa grafik ob’ektlarni o’zlashtirish va yaratish imkonini beruvchi past darajadagi funktsiyalar majmuasini taqdim qiladi. Bu tizim boshqariluvchi grafika (Handle Graphics) deyiladi. Grafik ob’ektlar - bu Matlabdagi boshqariluvchi grafika tizimining bazis elementlaridir. Ular ierarxik daraxt tuzilishli ko’rinishda bo’ladi. U orqali grafik ob’ektlar bog’lanishini ko’rish mumkin. Boshqariluvchi grafika ob’ektlarining 10 ta ko’rinishi mavjud:

* Root

* Figure

* Uicontrol

* Axes

* Uimenu

* Image

* Line

* Surface

* Text

* Light Har bir grafik ob’ekt o’zining handle(manipulyator) deb ataluvchi identifikatoriga ega. Bu identifikatorni Matlab ob’ekt yaratilganda qo’shib qo’yadi. Ayrim grafiklar, masalan, bir nechta egri chiziqlar grafiklari, har biri o’z identifikatoriga ega bo’lgan ob’ektlardan tashkil topadi. Barcha ob’ektlar xossalarga ega. Bu xossalar uni ekranga qanday chiqishini aniqlab beradi. Matlab tizimi operatorlari Matlab tizimining operatorlari uchta kategoriyaga bo’linadi:

• arifmetik operatorlar - hisoblashlarni bajaradi va arifmetik ifodalarni tuzish imkonini beradi.

• munosabat operatorlari - sonli operandlarni solishtirish imkonini beradi.

• mantiqiy operatorlar - mantiqiy ifodalarni tuzish imkonini beradi. Arifmetik operatorlarning bajarilish tartibi: (.’) (.^) (‘) (^) (+) (-) (.*) (./) (.\) (*) (/) (\) (+) (-) (:) Matlab tizimining arifmetik operatorlari bir xil o’lchovli massivlar bilan ishlaydi. Vektorlar va to’g’ri to’rtburchakli massivlar uchun ikkala operand ham bir xil o’lchovga ega bo’lishi kerak (skalyarlar bundan mustasno). Munosabat operatorlari: < > <= >= == ~= Munosabat operatorlari teng o’lchovli ikkita massivni elementlari bo’yicha solishtirishni bajaradi. Vektorlar va to’g’ri to’rtburchakli massivlar uchun ikkala operand ham bir xil o’lchovga ega bo’lishi kerak (skalyarlar bundan mustasno). Mantiqiy operatorlar: & | ~ Mantiqiy operatorlar teng o’lchovli massivlarni elementlari bo’yicha solishtirishni amalga oshiradi. Vektorlar va to’g’ri to’rtburchakli massivlar uchun ikkala operand ham bir xil o’lchovga ega bo’lishi kerak (skalyarlar bundan mustasno).

MathCad dasturi haqida umumiy tushunchalar

Bu kitobda Mathcad dasturi, uning dizayni va interfeysi haqida umumiy ma’lumotlar berilgan. Dasturning imkoniyatlari, afzallik tomonlari va misollar keltirilgan.

Mathcad-o’zi nima? Mathcad-universitet professor-o’qituvchilar, stajyorlar, tatqiqotchilar, aspirantlar, talabalar, texnik muxandislar, fiziklar, qolaversa barcha kasb egalari uchun hisoblash ishlarni bajaruvchi dastur ta’minoti hisoblanadi. Bu dastur bilan turli kasb egalari o’z sohasi bo’yicha masalalarni hal etishi va kerakli grafiklarni, diagrammalarni olishlari mumkin. Mathcad dasturini boshqacha qilib ayttanda dasturlash tili deyish mumkin. Mathcadda matematik tenglamalarni qog’ozga qanday yozilsa, ekranga ham shunday yoziladi. Bir vaqtning o’zida natijalarni ham olish mumkin. Foydalanuvchi bema’lol tenglamalariga ham izoh yozishi, 2 va 3 o’lchovli grafiklarni ham chizishi mumkin. Mathcad afzal tomonlaridan biri murakkab hisoblashlarni bajara olishi imkoniga ega. Foydalanuvchi masalasini, maqolasini, qolaversa barcha ilmiy ishlarini tayyorlashda ularni formatlash va chiroyli ko’rinishga keltirishda Mathcad ko’p imkoniyat yaratib beradi. Mathcad yuzdan ortiq o’zgaruvchili va konstantali chiziqli va chiziqsiz tenglamalar tizimi, matritsa va vektorlar ustida amallar, algebraik hisoblashlar, Laplas, Fur’e integrallari, massivlar, oddiy differentsial tenglamalar, chegaraviy shartlar, xususiy hosilali differentsial tenglamalar, polinomlarni tushuna oladi, ular ustida hisoblash ishlarini bajaradi. Mathcad ilmiy ishlarning natijalarni grafiklar bilan vizual qarashga imkon beradi. Foydalanuvchi funktsiyalarini osongina 2 va 3 o’lchovli grafiklarda turli ranglar, tumanli ko’rinishida, tekislikda tasvirlash imkoniga ega bo’ladi. Mathcad Help darchasidan foydalanishda ancha qulayliklar yaratilgan, bu ma’lumotnomadan kerakli ma’lumotlarni osongina qidirib topish mumkin. Zamonaviy komp’yutyer matyematikasi matyematik hisoblarni avtomatlashtirish uchun butun bir birlashtirilgan dasturiy tizimlar va pakyetlarni taqdim etadi. Bu tizimlar ichida Mathcad oddiy, yetarlicha qayta ishlangan va tyekshirilgan matyematik hisoblashlar tizimidir. Umuman olganda Mathcad – bu komp’yutyer matyematikasining zamonaviy sonli usullarini qo’llashning unikal kollyektsiyasidir. U o’z ichiga yillar ichidagi matyematikaning rivojlanishi natijasida yig’ilgan tajribalar, qoidalar va matyematik hisoblash usullarini olgan. Mathcad pakyeti muxandislik hisob ishlarini bajarish uchun dasturiy vosita bo’lib, u profyessional matyematiklar uchun mo’ljallangan. Uning yrdamida o’zgaruvchi va o’zgarmas paramyetrli algyebraik va diffyeryentsial tenglamalarrni yechish, funktsiyalarni tahlil qilish va ularning ekstryemumini izlash, topilgan yechimlarni tahlil qilish uchun jadvallar va grafiklar qurish mumkin. Mathcad murakkab masalalarni yechish uchun o’z dasturlash tiliga ham ega. Mathcad intyerfyeysi Windowsning barcha dasturlari intyefyeysiga o’xshash. Mathcad ishga tushurilgandan so’ng uning oynasida bosh myenyu va uchta panyel vositasi chiqadi: Standart (Standart), Formatting (Formatlash) va Math (Matyematika). Mathcad ishga tushganda avtomatik ravishda uning ishchi fayli Untitled 1 nom bilan ochiladi va unga Workshet (Ish varag’i) dyeyiladi. Standart (Standart) vositalar panyeli bir nyecha fayllar bilan ishlash uchun buyruqlar to’plamini o’z ichiga oladi. Formatting (Formatlash) formula va matnlarni formatlash bo’yicha bir nyecha buyruqlarni o’z ichiga oladi. Math (Matyematika) matyematik vositalarini o’z ichiga olgan bo’lib, ular yrdamida simvollar va opyeratorlarni fayli oynasiga joylashtirish uchun qo’llaniladi. Quyidagi rasmda Mathcadning oynasi va uning matyematik panyel vositalari ko’rsatilgan (1-rasm):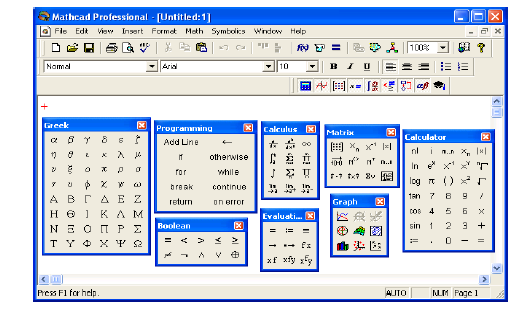

1-rasm. Mathcad pakyeti oynasi va uning matyematik panyel vositalari.

Colculator (Kol’kulyator) – asosiy matyematik opyeratsiyalar shabloni; Graph (Grafik) – grafiklar shabloni; Matrix (Matritsa) – matritsa va matritsa opyeratsiyalarini bajarish shabloni; Evluation (Baholash) – qiymatlarni yuborish opyeratori va natijalarni chiqarish opyeratori; Colculus (Hisoblash) – diffyeryentsiallash, intyegrallash, summani hisoblash shabloni; Boolean (Mantiqiy opyeratorlar) – mantiqiy opyeratorlar; Programming (Dasturlashirish) – dastur tuzish uchun kyerakli modullar yaratish opryeatorlari; Greek (Gryek harflari) - Symbolik byelgililar ustida ishlash uchun opyeratorlar.

Algebraik hisoblashlar

Boshlang’ich holatda ekranda kursor kryestik ko’rinishda bo’ladi. Ifodani kiritishda u kiritilaytgan ifodani egallab olgan ko’k burchakli holatga o’tadi. Mathcadning har qanday opyeratorini kiritishni uchta usulda bajarish mumkin:

✓ myenyu buyrug’idan foydalanib;

✓ klaviatura tugmalaridan foydalanib;

✓ matyematik panyeldan foydalanib. O’zgauvchilarga qiymat byerish uchun yuborish opyeratori “:=” ishlatiladi. Hisoblashlarni amalga oshirish uchun oldin formuladagi o’zgaruvchi qiymatlari kiritiladi, kyeyin matyematik ifoda yzilib tyenglik “=” byelgisi kiritiladi, natijada ifoda qiymati hosil bo’ladi (2-rasm). Oddiy va matyematik ifodalarni tahrirlashda myenyu standart buyruqlaridan foydalaniladi. Tahrirlashda klaviaturadan ham foydalanish mumkin, masalan kyesib olish – Ctrl+x; nusxa olish – Ctrl+c; qo’yish – Ctrl+v; bajarishni byekor qilish – Ctrl+z. Mathcad 200 dan ortiq o’zida qurilgan funktsiyalariga ega bo’lib, ularni matyematik ifodalarda ishlatish uchun standart panyel vositasidagi Insert Function (Funktsiyani qo’yish) tugmasiga bog’langan muloqot oynasidan foydalaniladi. Mathcad iga matn kiritish uchun bosh myenyudan Insert→Text Region (Qo’yish→Matn maydoni) buyrug’ini byerish yki yaxshisi klaviaturadan ikkitali kavichka (“) byelgisini kiritish kyerak. Bunda matn ma’lumotini kiritish uchun ekranda matn kiritish maydoni paydo bo’ladi. Matn kiritish maydoniga matyematik ifodani yzish uchun matyematik maydonni ham qo’yish mumkin. Buning uchun shu matn maydonida turib Insert→Math Region (Qo’yish→Matyematik maydoni) buyrug’ini byerish kifoya. Bu maydondagi kiritilgan matyematik ifodalar ham oddiy kiritilgan matyematik maydon kabi hisoblashni bajaradi.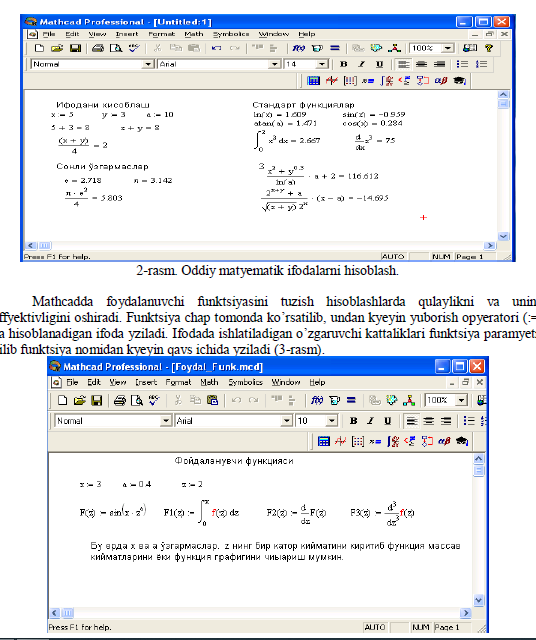

3-rasm. Hsoblashlarda foydalanuvchi funktsiyasini tuzish.

Diffyeryentsial tenglamalarrni yechish

Diffyeryentsial tenglamalarrni yechish ancha murakkab. SHu sabab Mathcadda barcha diffyerntsial tenglamalarrni ma’lum chyegaralanishlarsiz to’g’idan-to’g’ri yechish imkoniyati mavjud emas. Mathcadda diffyeryentsiallar tyenglama va tizimlarini yechishning bir nyecha usullari mavjud. Bu usullardan biri Odesolve funktsiyasi yrdamida yechish bo’lib, bu usul boshqa usullarga nisbatan eng soddasidir. Bu funktsiya Mathcad 2000 da birinchi bor yaratildi va u birinchi bor diffyeryentsial tyenglamani yechdi. Mathcad 2001da bu funktsiya yanada kyengaytirildi. Odesolve funktsiyasida diffyeryentsial tenglamalarr tizimini ham yechish mumkin. Mathcad diffyeryentsial tenglamalarrni yechish uchun yana ko’pgina qurilgan funktsiyalarga ega. Odesolve funktsiyasidan tashqari ularning barchasida, byerilgan tyenglama formasini yzishda ancha murakkablik mavjud. Odesolve funktsiyasi tyenglamani kiritish blokida oddiy diffyeryentsial tyenglamani o’z shaklida, xuddi qog’ozga yzgandyek yzishga imkon yaratadi (4-rasm). Odesolve funktsiyasi yrdamida diffyeryentsial tenglamalarrni boshlang’ich shart va chyegaraviy shartlar bilan ham yechish mumkin.

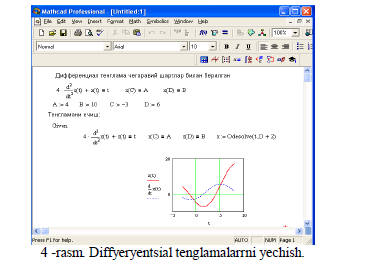
Byerilgan tyenglamani yozishda xuddi diffyeryentsiallash opyeratorini ishlatgan holda ham yki shtrixlar bilan ham yzish mumkin. Boshlang’ich shartni yzishda esa faqat shtrix bilan yzish kyerak va uni kiritish uchun Ctrl+F7 klavishilarni baravar bosish kyerak. Odesolve funktsiyasiga murojaat uch qismdan iborat hisoblash bloki yzuvini talab qiladi: Given kalit so’zi; Diffyeryentsial tyenglama va boshlang’ich yki chyegaraviy shart yki diffyeryentsial tenglamalarr tizimi va unga shartlar; Odesolve(x,xk,n) funktsiya, bu yerda x – o’zgaruvchi nomi, xk – intyegrallash chyegarasi oxiri (intyegrallashning boshlang’ich chyegarasi boshlang’ich shartda byeriladi); n – ichki ikkinchi darajali paramyetr bo’lib, u intyegrallash qadamlar sonini aniqlaydi (bu paramyetr byerilmasa ham bo’ladi. Unda qadamni Mathcad avtomatik ravishda tanlaydi). Diffyeryentsial tenglamalarr tizimini yechish uchun Odesolve funktsiyasi ko’rinishi quyidagicha: Odesolve( , x, xk, n)

Integrallash tenglamalarni yechish

Qiymatlarni global yuborish. Simvolli hisoblashlar Ayrim o’zgarmaslarga global qiymatni byerish uchun quyidagi protsyedurani bajarish kyerak bo’ladi:

1.O’zgarmas nomi kiritiladi.

2.Matyematika panyelidan Evaluation Toolbar (Baholash panyeli) tugmasi bosiladi.

3.Ochilgan Evaluation (Baholash) oynasidan Global Definition (Global aniqlash) tugmasi bosiladi yki Shift+ tugmalari baravar bosiladi. Bunday aniqlanish barcha lar uchun ta’sir qiladi, ya’ni barcha larda bu qiymatni ishlatish mumkin. Sonli hisoblashlardan tashqari Mathcad byelgili (simvolli) hisoblashlarni ham amalga oshiradi. Bu dyegani hisoblashlar natijasini analitik ko’rinishda tasvirlash mumkin. Masalan, aniqmas intyegral, diffyeryentsiallash va boshqa shu kabi masalalarni yechishda uning yechimini analitik ko’rinishda tasvirlaydi. Bunday oddiy simvolli hisoblashlar 5-rasmda kyeltirilgan.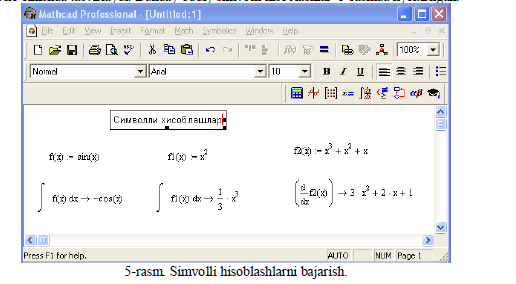

Simvolli hisoblashlarni bajarishda ikkita asosiy vosita mavjud: Symbolics (Simvolli hisoblash) myenyusi; Matyematika panyelidan Symbolic panyeli. Bu vositalar ancha murakkab simvolli hisoblashlarda qo’llaniniladi. Hozir esa oddiy simvolli hisoblashni bajarishning eng sodda usuli, ya’ni tyez-tyez ishlatilib turiladigan usullardan biri - simvolli tyenglik byelgisi (→) usulini ko’rib chiqamiz. Quyida bu usuldan foydalanishning kyetma-kyetlik tartibi byerilgan:

1. Matematika panyelidan Calculus Toolbar (Hisoblash panyeli) tugmasi bosiladi.

2. Ochilgan panyel oynasidan Calculus (Hisoblash) ni tanlab, aniqmas intyegralni sichqonchada chiqillatiladi (misol tariqasida aniqmas intyegral qaralayapdi).

3. Kiritish joylari to’ldiriladi, ya’ni funktsiya nomi va o’zgaruvchi nomi kiritiladi.

4. Simvolli byelgi tyengligi (→) byelgisi kiritiladi.

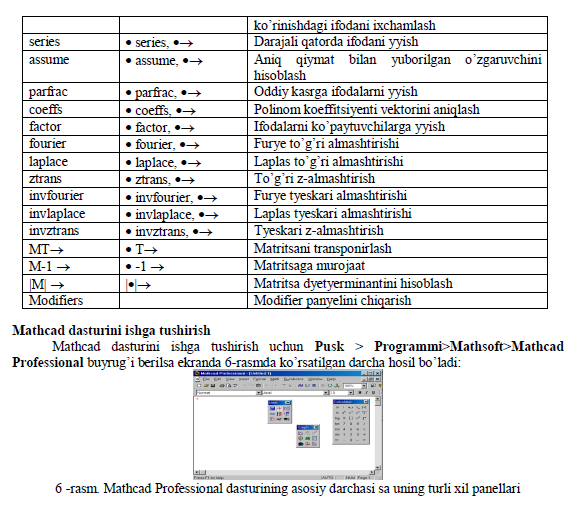
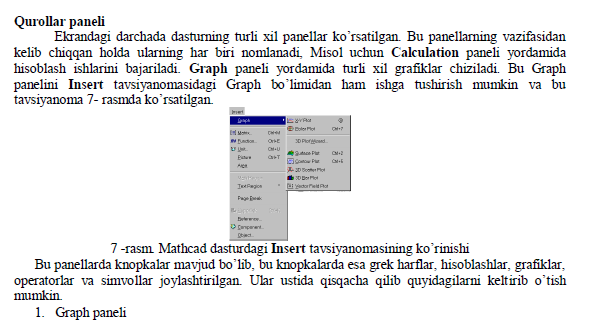
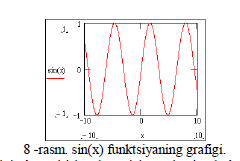
Grafikning o’lchamini o’zgartirish uchun sichqonchaning ko’rsatkichini grafikni ustiga olib borib, chap klavishini bosiladi. Grafikning hamma tomonlarida ramka va uning chetlarida qora kichkinagina kvadratlar paydo buladi. Shu kvadratlari ustiga sichqonning ko’rsatkichini olib borish kerak, birdaniga ko’rsatkichning ko’rinishi o’zgaradi. So’ngra esa sichqonchaning chap knopkasi bosiladi va knopkani quyib yubormay grafikning o’lchamini o’zgartirish mumkin. Yozgan va chizilgan grafiklarni ixtiyoriy joyga olib borish uchun sichqonchani ular ustiga bosilsa ko’rsatkich odamning qo’l shakliga o’zgaradi. Yana chap knopkani bosib kerakli joyga olib borib qo’yiladi.

Bir da bir necha funktsiyalarning grafiklarini chizish ham mumkin. Ekranga funktsiyalarni oldindan yozib olish kerak. So’ngra zsa Insert tavsiyanomasidagi Graph bo’limi tanlanadi va grafiklardan x va y koordinatalar (2 ulchovli) bo’yicha grafik ishga tushiriladi va ekranda koordinatali grafik hosil bo’ladi. Ramkani ichidagi kursor turgan joylarga x, y funktsiyalar yoziladi va Enter klavishi bosiladi. Birinchi grafik hosil bo’ladi. Yana Insert tavsiyanomasidagi Graph bo’limiga o’tiladi va grafiklardan qutb bo’yicha grafik ekranga chiqariladi va funktsiya oldingidek yozilsa 9- rasmdagi grafik hosil qilinadi: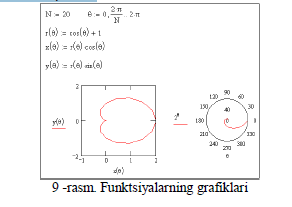

3 o’lchovli grafikni chizish

2 o’zgaruvchili va 3 o’zgaruvchili funktsiyalarning grafiklarni turli xil ko’rinishda chizish mumkin. Misol sifatida 2 o’zgaruvchili funktsiyaning grafigini chizish mumkin. M ni 20gacha tenglab, x va y lar uchun i va j larni 0 dan M gacha deb olinadi. So’ngra zsa x va y larni sin(x,y) ni qiymatlarini M matritsaga tenglab ekranga yoziladi. So’ngra esa Insert tavsiyanomasidagi Graph bo’limi tanlanadi va grafiklardan 3 o’lchovli grafik ishga tushiriladi. Ekranda 3 o’lchovli koordinatali ramka hosil bo’ladi. Kursor turgan joyga M ni yozish orqali 10 - rasmda ko’rsatilgan grafikni hosil qilish mumkin:

Nazorat savollari

1. Matematik modellashtirish deganda nima tushunasiz?

2. Modellashtirishning qanday afzalliklari va kamchiliklari bor

3. Matematik modellar tuzilish tamoyillariga ko‘ra nechi turga bo’linadi?

4. Matlab tizimi haqida tushuncha bering.

5. MathCad tizimi haqida tushuncha bering.

6. Matcad tizimi yordamida muaxassislikka oid masalalarning matematik modellarini amalga oshirish va qanday imkoniyatlarini bor?

7. MATLAB tizimida jarayonlarning imitatsion modellarini yaratish va amalga oshirish(Simulink paketi) mumkinmi?